Radian, a unit for angle called the “arc degree method”, is a unit. It was first introduced in the second grade of high school using the trigonometric function. It is mainly used in math and physics.
This page explains what radians are and how to convert them into degrees.
What is Radian?
Definition of the radian
The International System of Units (SI), the unit of plane angle, is the radian. It is described as follows.
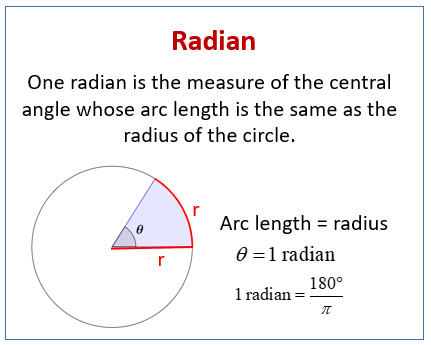
1 Radian is the magnitude for a central angle for an arch equal to the radius of a circle.
The unit symbol rad is the expression of an angle using this symbol as the unit. It is also known by the radian.
Even so, I find it difficult to understand an image by just listening to it once. Let’s look at the definition with figures.
An orange line in the figure below indicates an arc with a radius equal to its length. 1 radian indicates the magnitude of the central angle (orange corners) for this arc.1 radian diagram(1 radian57.2958deg)
Converting one radian to degrees (deg) produces a half-hearted number of approximately 57.2958deg. This number is actually infinite in terms of decimals.
This was a problem. Although you may feel that this is a difficult method to express an angle it is not. While the degree method may sometimes use 1deg ,…,, there is no way that radians can be separated by integers such as 1rad ,….. To represent the Angle, the basic P is used.
Next, I will discuss the conversion between radians (degrees) and radians.
By the by, Radians often don’t have the unit rad . Radians are the ratio of length of the circle to radius length, which is the length divided by the length. This is why the units cancel each others.
Radians: How to use them
Radians are useless if you only consider the ratio of the r,x,y to the angle with trigonometric functions.
It is used for linear approximation to angles (simplification or speeding up calculations), but it is not clear what radians means.
When differentiation occurs, Radians can shine.
The story doesn’t work when trigonometric function are involved in differentiation. ” degrees” is the main. ” Radians ” are the main.
We will explain the true use of Radians when we discuss differentiation of trigonometric function.
the angle value that deals with trigonometric operations on computers is in Radians. In radians, trigonometric operations are not only available in C language but also Excel. Although Unity of the game engine is displayed in units of degrees, because the program is written using C # and Math for calculation, it is still handled in units that are radians at its end. It is radian because it deals with trigonometric operations on a computer. However, one major reason is that series expansion (polynomial approximate) is performed in order to obtain extremely accurate calculation results.
You don’t have to be proficient in series expansion and differentiation to understand trigonometric functions. Understanding trigonometric operations in depth requires understanding differentiation. Understanding series expansion is essential for internal processing. But, when you are first dealing with trigonometric calculations, it suffices to convert the degrees to Radians.